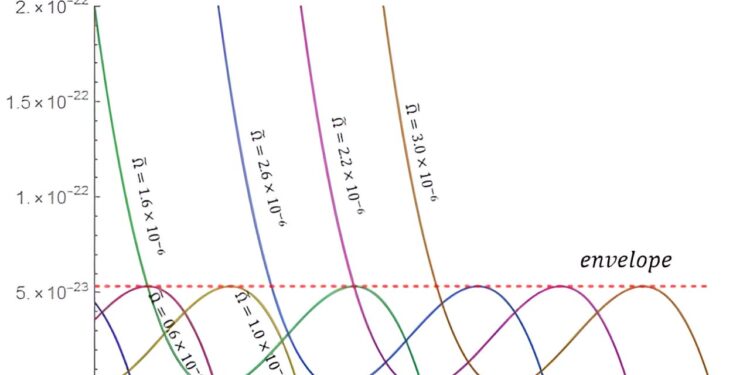
Excitation rates of atoms under different Ω. Credit: arXiv (2024). DOI: 10.48550/arxiv.2408.13016
How would atoms behave near a supermassive object? We know how atoms behave in conditions of extremely low gravity, such as on the surface of the Earth: they can move from a lower energy level to a higher one when an electron absorbs a photon or a nucleus absorbs a gamma ray, etc. But what happens if the atom is in a strong gravitational field, such as that found near a rotating supermassive black hole or a rotating neutron star?
Two scientists at the Beijing Research Center for Computer Science in China have determined that the amount of excitation would also depend on how fast spacetime is rotating around the massive object. In fact, they say, the inverse picture could be useful: Measuring changes in a set of excitations could be used to determine how fast spacetime is rotating, a phenomenon called frame dragging.
The results are published on the arXiv preprint server.
Frame dragging is a prediction of Einstein’s theory of gravity called general relativity. Just as a stationary black hole warps spacetime around it, resulting in an event horizon and an apparent singularity at its center, in 1918 Austrian physicists Josef Lense and Hans Thirring discovered that the rotation of a massive object would drag spacetime near it in the direction of the rotation.
Distance and angle measurements would thus be modified near the mass, and space and time could even be partly confused with respect to a distant observer.
Known as the Lense-Thirring effect, this effect exists even in the “weak field” limit of Einstein’s equations, just as it does in spacetime near a black hole’s event horizon, where gravity is not too strong (but stronger than on Earth).
NASA and other groups have found astronomical evidence of drag on the frame, but researchers say the measurements need to be refined. The rate at which drag spins depends on the mass’s angular momentum (how fast it’s spinning) and its mass, as well as its distance from it.
In this study, the scientists assumed a small mass (like an atom or other object with energy levels) surrounded by a simple quantum field that exists everywhere outside the central rotating mass.
The particles associated with the quantum field have zero spin (in the quantum mechanical sense); an example would be an electromagnetic field, where the force carriers of the field, the photons, have zero spin. Would the angular frequency of the frame drag be reflected in the excitation rate of an atom?
In the simpler case of a non-rotating black hole, the “Schwarzschild solution” to Einstein’s equations, there is no frame-dragging. It is known that an atom at rest would be excited by the Hawking radiation from the black hole, radiation emitted with the frequency spectrum of a black body that is released at the event horizon surrounding the black hole. The excitation rate of the atom contains information about the strength of the gravitational field at the event horizon.
However, for a massive rotating black hole, which has the so-called “Kerr solution” (which was only discovered in 1963), there is no real event horizon and no singularities. Kerr spacetime does exhibit frame-dragging, but an atom at rest would not be excited.
Unlike the Schwarzschild solution, the Kerr solution is an exact solution for the structure of spacetime, even for very large masses and strong gravity. Co-authors Rui-Chen Liu and C.P. Sun therefore studied the case of an atom moving in a circle at constant speed in Kerr spacetime.
They “quantized” the spin-zero field, that is, they treated it according to the rules of quantum mechanics (which are different from Maxwell’s famous equations that treat electromagnetic fields as classical fields, without photons or spin-zero particles). Putting it all together and working out the mathematics, the two discovered that an atom will be excited.
They also found that the excitation rate (the number of excitations per second) is the same as that of an atom immersed in a thermal bath (surrounded by energy) at a temperature proportional to the atom’s acceleration as it spins around. This is similar to the Unruh effect, in which an atom subjected to constant acceleration in a vacuum, even in a straight line, would see particles and a thermal bath with an extremely low but non-zero temperature.
To further their analysis, Liu and Son considered different excitation energies for atoms rotating at different speeds and at different distances from the central mass and found that the excitation rates all appeared between 0 and an upper limit for all values of the rotation frequency driving the frame.
They write: “The frame-dragging effect generates a distinct excitation rate for atoms undergoing circular motion.” This upper limit could be measured and the rotational speed of the frame-dragging rotational frequency could be deduced as well as the radius of the motion.
They note that their approach exploits the nonlocal properties of quantum fields, also called entanglement, using measurements that do not depend on traditional stellar calibration, which uses stars with known luminous properties to determine the quality and reliability of a telescope’s sensors.
More information:
Rui-Chen Liu et al, The Frame-Dragging Effect on the Excitation Rate of Atoms, arXiv (2024). DOI: 10.48550/arxiv.2408.13016
Journal information:
arXiv
© 2024 Science X Network
Quote:Using atomic excitations to measure the rotation of spacetime (2024, August 29) retrieved August 29, 2024 from
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without written permission. The content is provided for informational purposes only.