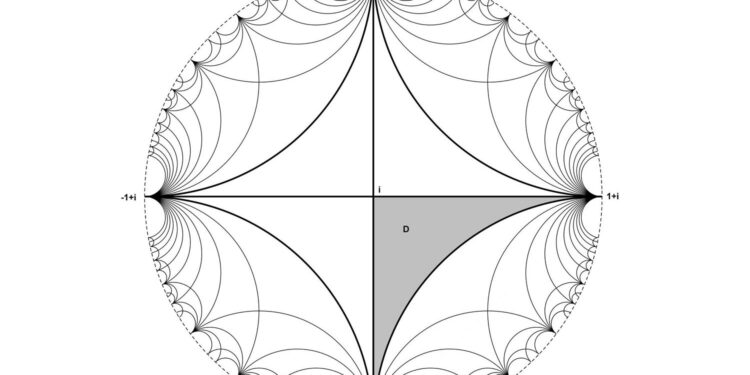
Mathematics meets aesthetics: Schweikart triangles produce patterns with an aesthetic appeal that inspires graphic designers and architects alike. Credit: Heinrich Begehr
In a recent study, mathematicians at Freie Universität Berlin demonstrated that plane tiling, or paving, is much more than a way to create a pretty pattern. Consisting of a surface covered with one or more geometric shapes without gaps or overlaps, tilings can also be used as a precise tool for solving complex mathematical problems.
This is one of the main conclusions of the study entitled “Beauty in/of mathematics: tessellations and their formulas”, written by Heinrich Begehr and Dajiang Wang and recently published in the scientific journal Applicable analysis. The study combines results from the field of complex analysis, the theory of partial differential equations and the theory of geometric functions.
One of the central themes of the study is the “principle of prosecutorial reflection”. This refers to the use of repeated reflections of geometric shapes at their edges to tile a plane, resulting in highly symmetrical patterns. Aesthetic examples of planar tilings can be seen in the work of MC Escher. Beyond its visual appeal, the principle has applications in mathematical analysis, for example as a basis for solving classical boundary value problems such as the Dirichlet problem or the Neumann problem.
“Our research shows that beauty in mathematics is not only an aesthetic notion, but also something deep and structurally effective,” explains Professor Begehr. “While previous research on tilings has largely focused on how shapes can be used to tile or cover a surface (for example, some well-known work by Nobel laureate Sir Roger Penrose), using the parquet reflection method to generate new tilings opens up new possibilities.
“It is a practical tool for developing ways to represent functions within these tiled regions, which could be useful in fields such as mathematical physics and engineering.”
In particular, it can be used to derive specific formulas for kernel functions, including the Green, Neumann, and Schwarz kernels, some of the tools that can be used to solve boundary value problems in physics and engineering. As such, this work creates an elegant connection between geometric intuition and analytical precision.
The principle of floor-thinking has been growing in popularity for over a decade and is particularly popular as a research topic among early-career researchers. Since its initial development, a total of fifteen theses and senior theses at Freie Universität have explored the topic, along with a further seven theses written by foreign researchers.
Remarkably, the principle works not only in Euclidean space, but also in hyperbolic geometries, those used in theoretical physics and in modern visualizations of space-time. Interest in the principle remains high. Last year, Begehr published a paper, “Hyperbolic Tessellation: Harmonic Green Function for a Schweikart Triangle in Hyperbolic Geometry,” in the journal Complex variables and elliptic equations in which he demonstrated the use of the parquet-reflection principle to construct the harmonic Green’s function for a Schweikart triangle in the hyperbolic plane.
“We hope that our results will resonate not only in pure mathematics and mathematical physics,” says Wang, “but may even inspire ideas in fields like architecture or computer graphics.”
All first thoughts. Credit: Applicable analysis (2025). DOI: 10.1080/00036811.2025.2510472
The tradition of tiling in Berlin
For almost two decades, the research group led by Begehr at the Institute of Mathematics at Freie Universität Berlin has been studying so-called “Berlin mirror tiles”, a method based on the principle of unified reflection developed by the Berlin mathematician Hermann Amandus Schwarz (1843-1921).
In this approach, a circular polygon (a shape whose edges are made up of pieces of straight lines and circular arcs) is reflected repeatedly until the entire plane is completely and seamlessly, without any overlaps or gaps. These models are not only visually striking, but also enable explicit integral representations of functions, a key tool for solving complex boundary value problems.
“Mathematicians once had to use a three-part vanity mirror to produce an infinite sequence of images,” says Begehr. “Nowadays, we can use iterative computer programs to generate the same effect, and we can complement that with exact mathematical formulas used in complex analyses.”
Schweikart triangles and hyperbolic beauty
Although considered very aesthetically impressive, tilings in hyperbolic spaces, for example in a circular disk, represent a particular challenge for mathematicians. This is where “Schweikart triangles” come in: special triangles with one right angle and two zero angles, named after the amateur mathematician and law professor Ferdinand Kurt Schweikart (1780-1857).
These triangles allow the complete and even tiling of a circular disk, producing patterns with an aesthetic appeal that offers new inspiration to graphic designers and architects. At the same time, the underlying mathematical constructs are very complex and require advanced analytical methods.
Mathematics as a visual science
The team’s findings highlight an often overlooked aspect of mathematics: it is not only an abstract discipline, but also a visual science in which structure, symmetry and aesthetics play a central role. When combined with modern visualization techniques, graphics software and digital tools, this information becomes even more relevant.
More information:
H. Begehr et al, Beauty in/of mathematics: tilings and their formulas, Applicable analysis (2025). DOI: 10.1080/00036811.2025.2510472
Provided by Freie Universitaet Berlin
Quote: When mathematics meets aesthetics: tilings as a precise tool for solving complex problems (October 10, 2025) retrieved on October 11, 2025 from
This document is subject to copyright. Except for fair use for private study or research purposes, no part may be reproduced without written permission. The content is provided for informational purposes only.