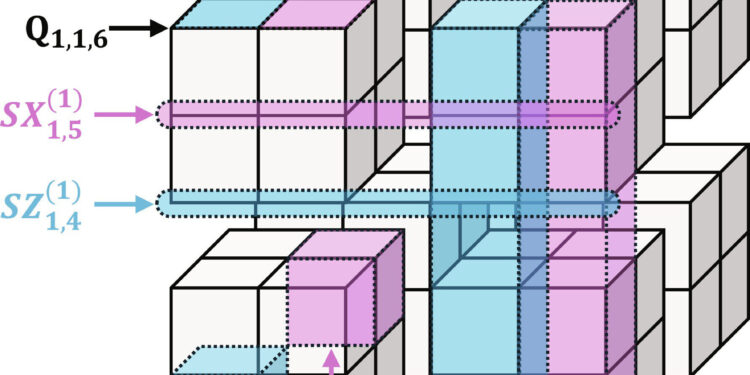
Visualization of the structure of the level 3 multi-hypercube code. Credit: Scientific progress (2024). DOI: 10.1126/sciadv.adp6388
In a work published in Scientific progressHayato Goto of the RIKEN Center for Quantum Computing in Japan has proposed a new approach to quantum error correction using what he calls “multi-hypercube codes.”
This approach, which turns out to have elegant geometry, could help achieve extremely efficient error corrections and contribute to highly parallel methods that will enable fault-tolerant quantum computing, the next step in the evolution of quantum computers.
According to Goto, “Thanks to recent experimental progress, there is now great hope that we can build fault-tolerant quantum computers, that is, quantum computers that can correct errors and outperform classical computers on certain tasks. But to achieve this, it is important to develop efficient quantum error correction.”
Over the past few decades, scientists have proposed many different methods for error correction. The conventional approach to quantum error correction typically relies on encoding a single logical qubit (a qubit being the equivalent of a bit on a classical computer) onto many entangled physical qubits, and then using a decoder to recover the logical qubit from the physical qubits.
However, the scalability of this approach is problematic, as the number of physical qubits required increases dramatically, leading to huge resource expenditures. To overcome this problem, high-throughput quantum codes, such as low-density parity-check quantum codes, have been considered.
With this approach, the logic gates that make the computations possible must be configured in a fairly sequential manner rather than completely parallel, making them less time efficient.
To address this problem, Goto proposed using an approach he calls “multiple hypercube codes.” It’s a method with a complicated name—high-throughput concatenated quantum codes—and it’s innovative in that the logical qubits can be mathematically visualized as forming what’s called a “hypercube”—a type of shape that includes squares and cubes as well as higher-order shapes such as the tesseract.
The beautiful mathematical and geometric structure of the code is remarkable, because most high-speed quantum codes have complex structures.
Goto points out that for the new codes to produce higher performance, he had to develop a new dedicated decoder that could interpret the output of the physical qubits. This innovative technique relies on level-by-level minimum distance decoding, which achieves high performance.
Unlike other similar methods, it also allows logic gates to be placed in parallel rather than in series, making the system analogous to the parallel processing of classical computers, leading Goto to call it “high-performance fault-tolerant computing” by analogy with “high-performance computing” which is used for massively parallel computing.
The work paid off. The codes achieve an encoding rate (a number that indicates the ratio of logical to physical qubits) of up to 30%, which Goto says appears to be the highest in the world among codes used for fault-tolerant quantum computing. And even at this high rate, the performance is comparable to that of classical codes at low rates.
Goto says: “In practice, this code could be implemented with physical qubit systems such as laser-trapped neutral atom qubits.”
More information:
Hayato Goto, High-performance fault-tolerant quantum computing with multiple hypercube codes, Scientific progress (2024). DOI: 10.1126/sciadv.adp6388
Quote:New quantum error correction method uses ‘multiple hypercube codes’ while exhibiting beautiful geometry (2024, September 6) retrieved September 7, 2024 from
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without written permission. The content is provided for informational purposes only.