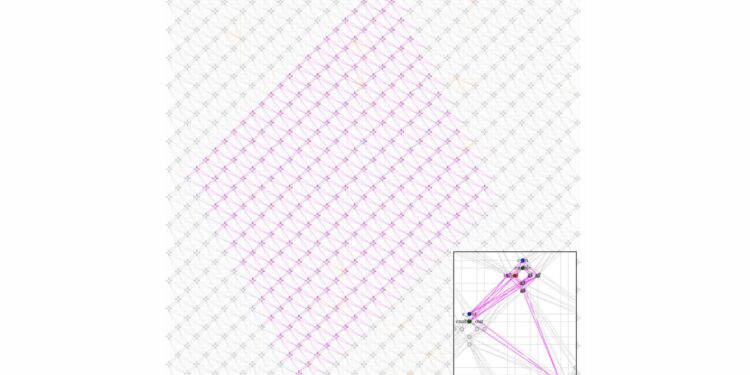
Gray dots/lines: 5,760-qubit Pegasus topology from Advantage 4.X QA (courtesy of D-Wave). Purple dots/lines: subgraph used by the most space-efficient modular encoding for a 21×12-bit multiplier mentioned in the study. Orange dots/lines: faulty qubits and couplings in the hardware of the Advantage 4.1 machine used in the study. Credit: Jingwen Ding et al.
Researchers at the University of Trento, Italy, have developed a new approach to prime factorization via quantum annealing, exploiting a compact modular coding paradigm and enabling the factorization of large numbers using D-Wave quantum devices.
Prime factorization is the procedure of breaking down a number into its prime components. Any integer greater than one can be uniquely expressed as a product of prime numbers.
In cryptography, prime factorization is of particular importance because of its relevance to the security of encryption algorithms, such as the widely used RSA cryptosystem.
The prime factorization process becomes difficult due to the nature of prime numbers, and it becomes even more complicated as the numbers considered become larger, leading to a large number of possibilities to consider.
The inability to efficiently factor large numbers ensures the integrity of encrypted communications. The robustness of these cryptographic systems relies on the computational complexity of prime factorization, making it a crucial element in protecting sensitive information in the digital age.
If someone can efficiently factor the product of two large prime numbers, they could potentially break the security of cryptographic systems. Understanding and advancing prime factorization techniques helps ensure the robustness of cryptographic protocols and protect sensitive information in digital communications.
In a new study published in Scientific reports, researchers led by Professor Roberto Sebastiani from the University of Trento, Italy, aimed to tackle this process using quantum annealing. The team also consisted of Jingwen Ding and Giuseppe Spallitta, Ph.D. students at the University of Trento.
“As a computer scientist who has spent an entire career developing classical procedures to solve complex computational logic and optimization problems, I was very intrigued by the idea of tackling a technology such as quantum annealing based on a computing paradigm very different from anything I had encountered before,” says the professor. “, Sebastiani told Tech Xplore.
Quantum annealing
Quantum computers are particularly suited to prime factorization problems because of their ability to perform parallel calculations and exploit quantum phenomena. Specifically, quantum annealers, like those in D-Wave, are designed to solve optimization problems by simultaneously searching for optimal solutions among a large number of possibilities.
In the context of prime factorization, where the search for prime factors involves the rapid exploration of many combinations, the parallelism inherent in quantum computing offers a potential advantage.
Quantum annealers exploit quantum phenomena such as quantum superposition and quantum tunneling to explore multiple solutions simultaneously, making them well suited to prime factorization problems. This parallel exploration of possibilities can significantly improve the efficiency of prime factor search compared to classical algorithms.
Compact encoding
Research has a dual nature. In the first aspect of their work, the researchers achieved a breakthrough by developing a compact modular encoding of a 21 × 12-bit binary multiplier circuit directly into a single 8-qubit module within the Pegasus topology of quantum annealers of D -Wave.
Think of the Pegasus topology as a web connecting qubits, determining how data flows.
“The game-changer in this work, which turned out to be a positive surprise for us, was the successful encoding of a controlled full adder (CFA) subcircuit into a single 8-qubit module of the Pegasus Quantum Annealer topology,” explained Professor Sebastiani.
Schematic of a 4×4 modular multiplier with 16 CFA modules. Credit: Scientific reports (2024). DOI: 10.1038/s41598-024-53708-7
CFA is a quantum subcircuit that performs 1-bit addition operations under specific control conditions, which the team encoded into an annealing topology module using optimization module theories ( OMT), a technology combining logical reasoning and optimization.
Unlike previous approaches that neglected the layout of the system, the team used OptiMathSAT, its Optimization Modulo Theories tool, to create coding that is well aware of the topology. This demonstrated the effectiveness of their approach and marked a significant advance in coding techniques for quantum annealing.
The modularity of their encoding approach is a game-changer. They demonstrated the ability to code in annealing the factorization of a number up to 8,587,833,345 into the product of two prime numbers, 2,097,151 and 4,095. This is the largest factorization problem ever coded in quantum annealing using their new method.
“We noticed two key facts. We can decompose an n × m bit multiplier circuit into a matrix of interconnected CFA subcircuits and we can align it with the Pegasus array of 8-qubit modules,” explained Professor Sebastiani .
This allowed the researchers to create a structure that can effortlessly scale as the number of qubits in future quantum annealing chips grows.
Experimental factorization
In the second phase of their research, the team conducted an extensive experimental evaluation on a D-Wave Advantage 4.1 quantum annealer. The aim was to study the actual solving of coded FP problems and to evaluate the capabilities of quantum annealing in practice.
“Overall, due to faulty qubits and limited QUPU time resources, 8,219,999 = 32,749 × 251 was the highest prime product we were able to factor. To our knowledge, this is the highest “large number ever factored using a quantum device without relying on external search or preprocessing procedures run on classical computers,” explained Professor Sebastiani.
This achievement has significant implications for quantum computing and its applications. The researchers demonstrated advances in solving complex computational problems, proving that substantial progress is possible even with the limitations of current quantum annealing hardware.
One of the challenges of this work is that since each prime factorization problem has at most two solutions (e.g., 35=7×5 or 35=5×7), quantum annealing must search for these global minima in an exponentially large solution. . space.
Professor Sebastiani explained: “It’s like looking for a needle in a haystack. Fortunately, many annealing techniques and tricks are available to solve these problems, but it took a lot of practice to achieve satisfactory results.”
Beyond factorization
Professor Sebastiani highlighted the possibility of extending the use of these devices beyond prime factorization, considering applications in coding and checking the satisfiability of various circuits.
“We believe that quantum anneals can be used to encode and verify the satisfiability of many other interesting circuits. Thus addressing the propositional satisfiability of Boolean circuits (SAT) – a much more general problem than prime factorization and allows representing a variety of real realities. -global problems,” Professor Sebastiani shared.
Looking ahead, the researchers highlighted the importance of developing hybrid quantum-classical procedures, in which annealing can be invoked by classical procedures to solve small but computationally very difficult combinatorial subproblems.
However, it is crucial to note that despite the remarkable achievements presented in their paper, the researchers remain cautious about the limitations. They point out that they are still far from solving prime factorization problems large enough to compromise the security of current cryptographic systems.
More information:
Jingwen Ding et al, Efficient first factorization via quantum annealing by locally structured modular integration, Scientific reports (2024). DOI: 10.1038/s41598-024-53708-7
© 2024 Science X Network
Quote: Quantum annealing and the future of prime factorization (February 21, 2024) retrieved February 21, 2024 from
This document is subject to copyright. Apart from fair use for private study or research purposes, no part may be reproduced without written permission. The content is provided for information only.