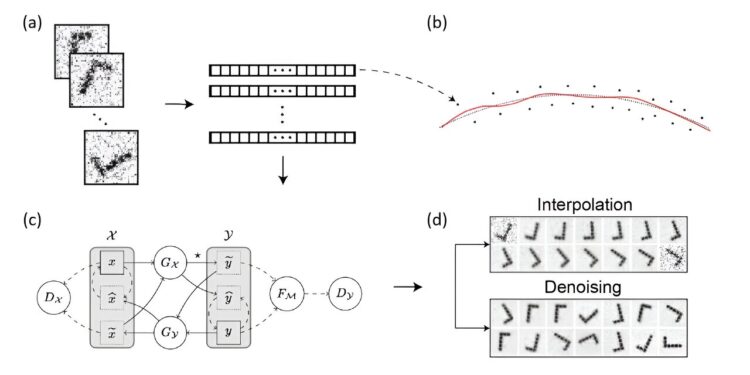
Illustration of latent manifold fitting using the Cycle Generative Adversarial Network (CycleGAN). CycleGAN is a deep learning technique for unsupervised image-to-image translation. In the real world, data, such as the images shown in panel (a), are often high-dimensional vectors. These vectors generally reside around a low-dimensional latent manifold, represented by the black dotted curve in panel (b). The CycleGAN framework, detailed in panel (c), efficiently learns to estimate this latent manifold (illustrated by the red curve in panel (b)). This advancement facilitates nonlinear interpolation and denoising in high-dimensional ambient space (panel (d)), providing significant improvements in data processing and analysis. Credit: Proceedings of the National Academy of Sciences (2024). DOI: 10.1073/pnas.2311436121
Statisticians from the National University of Singapore (NUS) have introduced a new technique that accurately describes high-dimensional data using smooth, lower-dimensional structures. This innovation marks a significant step forward in solving the challenges of complex nonlinear dimensional reduction.
Traditional data analysis methods often rely on Euclidean (linear) dependencies between features. Although this approach simplifies data representation, it struggles to capture the underlying complex patterns in high-dimensional data, typically located near low-dimensional manifolds.
To fill this gap, multiple learning techniques have emerged as a promising solution. However, existing methods, such as multiple integration and denoising, have been limited by the lack of detailed geometric understanding and strong theoretical foundations.
The team, led by Associate Professor Zhigang Yao of the Department of Statistics and Data Science, NUS, who holds a Ph.D. Student Jiaji Su pioneered a new method to efficiently estimate low-dimensional manifolds hidden in high-dimensional data. This approach not only achieves state-of-the-art estimation accuracy and convergence rates, but also improves computational efficiency through the use of deep generative adversarial networks (GANs).
This work was carried out in collaboration with Professor Shing-Tung Yau from the Yau Mathematical Sciences Center (YMSC) of Tsinghua University. Part of the work comes from Professor Yao’s collaboration with Professor Yau during his sabbatical visit to the Center for Mathematical Sciences and Applications (CMSA) at Harvard University.
Their conclusions were published in the form of a methodological document in the Proceedings of the National Academy of Sciences.
Professor Yao delivered a 45-minute guest lecture on this research at the recent International Congress of Chinese Mathematicians (ICCM) held in Shanghai from January 2-5, 2024.
Highlighting the importance of this work, Professor Yao said: “By fine-tuning the manifolds, we can reduce the dimensionality of the data while preserving crucial information, including the underlying geometric structure. This represents a major advancement in data analysis, improving both accuracy and efficiency. By providing a solution that overcomes the limitations of previous methods, our research paves the way for improved data analysis and offers valuable insights for various applications in the scientific community.
Looking ahead, Yao’s research team is developing a new framework to deal with even more complex data, such as single-cell RNA sequence data, while continuing to collaborate with the YMSC team. This ongoing work promises to revolutionize the approach to reducing and processing complex data sets, potentially providing new insights into a wide range of scientific fields.
More information:
Zhigang Yao et al, Manifold fitting with CycleGAN, Proceedings of the National Academy of Sciences (2024). DOI: 10.1073/pnas.2311436121
Provided by the National University of Singapore
Quote: A multiple fitting approach for high-dimensional data reduction beyond Euclidean space (January 29, 2024) retrieved January 29, 2024 from
This document is subject to copyright. Except for fair use for private study or research purposes, no part may be reproduced without written permission. The content is provided for information only.